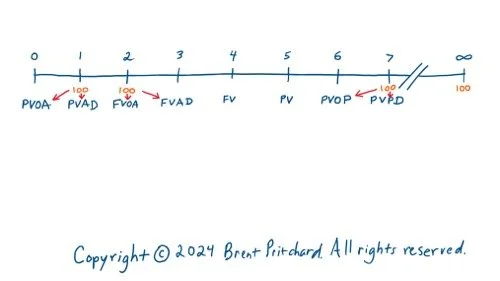
The Perfect Timeline.
Recently, our daughters were surprised to find out that their dad was awarded an art scholarship right out of high school. I’ve always had a creative side.
In college, my fellow art classmates used to like to razz me about selling out as I packed up my supplies and prepared to walk to my business classes. It was all in good fun. Looking back, I’ve always looked for balance in life in one way or another. This was just that.
In your finance classes, you might hear an instructor say something along the lines of, “When in doubt, draw a timeline.”
Now there’s no doubt in my mind that what follows just might be The Perfect Timeline. I’m not referring to straight lines or symmetry; rather, an illustration that can help business students see how the Building Block Time Value of Money equations interact with the timeline and specific payments. Behold, The Perfect Timeline:
There are a few things to point out. First, note how the tip of the arrow resembles the letter V. This reminds us where the (Present or Future) Value is under the timeline in relation to the first or last payment for an annuity and the first payment for a perpetuity. The abbreviations are as follows:
Present Value of an Ordinary Annuity (PVOA);
Present Value of an Annuity Due (PVAD);
Future Value of an Ordinary Annuity (FVOA);
Future Value of an Annuity Due (FVAD);
Present Value of an Ordinary Perpetuity (PVOP);
Present Value of a Perpetuity Due (PVPD);
And last but not least, Future Value (FV) and Present Value (PV).
The Perfect Timeline requires that you have a certain level of comprehension with regard to the Building Block Time Value of Money equations and how a lump-sum or single payment is different from an even series, etc.
Assuming a 5% true investment yield, which is what some might call a compound interest rate, can you find the following values:
PVOA: 185.94 (euro)
PVAD: 195.24 (euro)
FVOA: 205 (euro)
FVAD: 215.25 (euro)
PVOP: 2,000 (euro)
PVPD: 2,100 (euro)
FV of the FVAD: 226.01 (euro)
PV of the PVPD: 1,904.76 (euro)
Now consider the following:
The timeline is silent with regard to the time span in between periods or payments. This was on purpose to illustrate a point. Does the space in between each time period marker represent one year, six months, a quarter, a month, a week? This is an important question, because you can’t compound or discount moneys below the timeline unless you have an “i” that matches “n.” Enter the last of the Building Block Time Value of Money equations: the True Investment Yield equation.
Notice how we could add a “1” to each time period marker and consider a different range of time.
If you’re running the numbers using the building block Time Value of Money equations for an annuity, pay attention to the relationship between “N” and “PMT.”
Did you catch that for the FVOA the second in the series of two even payments doesn’t earn a return on investment.
For those fluent with the building block Time Value of Money equations for an annuity or perpetuity, see how the add-on expression, (1 + i), just moves the PVOA and FVOA and PVOP one period into the future to calculate the PVAD and FVAD and PVPD, respectively. As it relates to the future value associated with the even series with two even payments that last payment gets its turn to earn a return on investment, and the other payment gets to “work” for one more period.
Notice how the PVOA is as of one period before the first even payment in the series.
See how FVAD can sub-in for PV in the Building Block Future Value equation. Sooner or later, the future becomes the present!
If you’re doing the work and putting in the reps, first I congratulate you for getting this far! Now, did you notice how for the PVPD or PVOP the value of the investment is maintained at $2,000. For the PVPD, do you understand that the 100 (euro) payment happens right way, thus reducing the amount of money invested from 2,100 to 2,000 (euro). And finally, for the PVOP, do you understand that the 2,000 (euro) investment earns a return on investment for one period before the first payment in the series is made.
Notice how the PV doesn’t need to be as of (t)o(day) or (n)o(w); i.e., time period marker zero on the timeline.
There you have it, The Perfect Timeline. I don’t think our illustrator is going to be worried about not hearing from us again! Forget about it!
What do you think?
Brent Pritchard is an author and college finance lecturer with over two decades of industry experience and cofounder of Boxholm Press, LLC, a family-owned-and-operated publishing company providing educational content, products, and services. He pioneers an innovative and approachable new way of learning and teaching the Time Value of Money as well as thought leadership in other business topics. His most recent book is Would Your Boomerang Return? You can contact him on his website here.